Batch 3 - Class 118 - Swapping Hats, Facebook Friends
Pre-Class Problem:
- In the jenga problem, what would happen if an ornament was to be hung 1/4 the distance from the extreme edge of first block, and the ornament weight was 1/5 the weight of the block
- This additional torque of 1/5(f(n)-1/4) now needs balancing, so the above equation can be adjusted accordingly
Attendance: Nandini, Aneyaa, Khushi, Anshi, Ahana, Palak, Arnav, Damini, Siddhant, Arnav, Anishka, Zorawar, Liza, Diya
Class Notes:
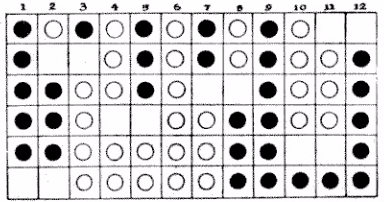
Swapping Hats (Dudeney - 236)
Ten hats were hung on pegs as shown in the illustration below - five silk hats and five felt hats. Two pegs at the end of the row are empty.

You have to remove two contiguous hats and place them in the same order on the two empty pegs. Repeat this process till the hats again hang in an unbroken row, but with all the silk hats together and all felt hats together.
- Instructor Notes: Get kids to think how they start to bring similar hats together. May be get kids to try 6 hats first (Answer in 4 moves - Move positions 2,3 then 5,6 then 7,8 and then 1,2)
- Answer:
Swapping Kids (Dudeney - 237)
Now lets assume there are eight boys and girls are sitting as illustrated below.
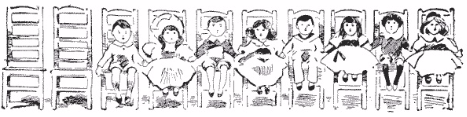
You have to remove two contiguous kids and place them on the empty chairs, but in reverse order relative to how you picked. Repeat the process till you can get all the boys together and all the girls together, with two vacant chairs at one end.
- Answer:

Facebook Friends
What is the least number of people on facebook, so that there are at least three people who are all friends of each other, or none of the three are friends with each other
- Instructor Notes: Let kids guess - ask them to justify their intuition. What if we wanted at least two people who were all friends or all enemies?
- Lets start to solve it methodically - from 2 people onwards, and see if we can find examples where this is not true
- Answer 6. We can show that upto 5, there is a case where none of the conditions are satisfied. If we consider the 6th entrant, the 6th entrant is either friends or not-friends with at least 3 people. Take that set of three. If they are all friends/not-friends then we are done. If any pair is/is-not then we can combine with the new entrant to get that trio.
The picture below shows all the 78 possible friends-stranger graphs with 6 nodes. For each graph, the triplet is shown.

Homework
Two people have asked you out for a date and you've decided to decide who to go with by flipping a coin. The problem is that the only coin you have is biased: you know that heads comes up with a probability of 0.75 rather than 0.5 as is the case with a fair coin. However, you do really want each of the two people to have a fair chance of being picked. Using a combination of two coin flips instead of one, can you find a way of making the random decision fair?(Hint: the chance doesn't have to be 50:50.)
- Answer: Go with A if you get heads followed by tails. Go with B if you get tails followed by heads. If you get two heads or two tails, try again for two throws.
- Follow up: what if the probability of heads was 0.6 instead of 0.75?
References:
https://ia902701.us.archive.org/4/items/AmusementsInMathematicspdf/AmusementsInMathematics.pdf - Dudeney